Implementando una ALU - CS02
En esta ocasión el objetivo es implementar una ALU (Arithmetic-Logic-Unit) la cual es una parte fundamental de nuestra CPU que se encarga de realizar operaciones aritmeticas y logicas, para ello iremos implementando progresivamente otros chips que son necesarios y tenemos la restricción de que solo se pueden usar CHIPS previamente implementados.
Los chips que deben ser implementados son:
- Half Adder
- Full Adder
- 16-bit Adder
- 16-bit Incrementer
- Arithmetic Logic Unit (ALU)
Tabla de contenidos
- Tabla de contenidos
- Conocimientos importantes
- Complemento a 2
- Identificando los numeros negativos en n-bits usando complemento a 2 (reto 2)
- El rango de valores representables en n-bits usando complemento a 2 (reto 1, 3, 4)
- Sumas y restas usando complemento a 2 (reto 5, 6, 7)
- Los computadores y el complemento a 2 (reto 8)
- Diferencias entre un half adder y un full adder (reto 9)
- Significado del carry de una suma (reto 10)
- Implementando el half adder
- Implementando el full adder
- Implementando el 16-bit Adder
- Implementando el 16-bit Incrementer
- Implementando la ALU
- Lista de chequeo y autoevaluacion
Table of contents generated with markdown-toc
Conocimientos importantes
Complemento a 2 - concepto1
El complemento a 2 se puede ver como una tecnica que me permite representar numeros negativos en binario, existen varias formas de hallarlo:
Por ejemplo si tenemos el 2 en 4 bits (0010) y queremos hallar como se representaria el -2, podriamos hallar el complemento a 1 de 0010 es decir ~0010=1101 (Negación bit a bit) y luego a ese resultado sumarle un 1 (0001), 1101+0001=1110, lo cual quiere decir que el -2 se representa como 1110 en complemento a 2 de 4-bits.
Cabe decir que tambien se puede usar el complemento a 2 para hacer el proceso contrario, es decir, sea la representación de un numero negativo en complemento a 2, ¿cual es la representación positiva de dicho numero?
(~1110)+0001=0001+0001=0010 (2 en base_10)
En la representación mediante complemento a 2, los numeros positivos son simplemente representados como ellos mismos, mientras los negativos son representados por el complemento a 2 de su valor absoluto.
Otra forma de calcular el complemento a 2 de un numero es mediante la siguiente ecuación:
Donde:
- N: El numero al cual le queremos calcular el complemento a 2
- n: Cantidad de digitos binarios
Nota: Complemento a 2 y representación mediante complemento a 2 son dos cosas distintas, el primero es una funcion matematica, mientras que el segundo es una tecnica que se puede usar para representar numeros negativos usando la funcion matematica complemento a 2.
| Numero (N) | Numero de digitos (n) | Funcion complemento a 2 de X=Abs(N) (2^n - X) | Representación mediante complemento a 2 |
|---|---|---|---|
| 1 | 8 | NA | 0000 0001 |
| 0 | 8 | NA | 0000 0000 |
| -1 | 8 | 1111 1111 | 1111 1111 |
| -128 | 8 | 1000 0000 | 1000 0000 |
| 127 | 8 | NA | 0111 1111 |
| 128 | 8 | NA | Overflow Error |
| -130 | 8 | ERROR | Overflow Error |
Identificando los numeros negativos en n-bits usando complemento a 2 - concepto2
| Numero base 10 | Complemento a 2 8-bits | Complemento a 2 16-bits |
|---|---|---|
| 6 | 0000 0110 | 0000 0000 0000 0110 |
| 5 | 0000 0101 | 0000 0000 0000 0101 |
| 4 | 0000 0100 | 0000 0000 0000 0100 |
| 3 | 0000 0011 | 0000 0000 0000 0011 |
| 2 | 0000 0010 | 0000 0000 0000 0010 |
| 1 | 0000 0001 | 0000 0000 0000 0001 |
| 0 | 0000 0000 | 0000 0000 0000 0000 |
| -1 | 1111 1111 | 1111 1111 1111 1111 |
| -2 | 1111 1110 | 1111 1111 1111 1110 |
| -3 | 1111 1101 | 1111 1111 1111 1101 |
| -4 | 1111 1100 | 1111 1111 1111 1100 |
| -5 | 1111 1011 | 1111 1111 1111 1011 |
| -6 | 1111 1010 | 1111 1111 1111 1010 |
| … | … | … |
En esta imagen hay dos puntos importantes a notar: 1) si tomamos un numero negativo, por ejemplo -1 y lo escribimos en complemento a 2 de 8 bits vemos que todos sus bits estan en true, y si luego lo representamos en un complemento a 2 de 16-bits los 8 bits extra siguen teniendo un valor de 1, es decir, no importa la cantidad de bits con la que representemos un numero negativo (o positivo) el complemento a 2 funcionará correctamente mientras se intente representar un número en el rango posible.
La segunda observación, es que vemos que si un numero es menor a 0 (negativo) el bit mas significativo (MSB) es 1 siempre en cambio cuando sea mayor o igual a 0 el MSB siempre es 0, aunque esta tabla no tenga todos los posible valores, si vemos una tabla completa se puede verificar la afirmación mencionada.
El rango de valores representables en n-bits usando complemento a 2 - concepto3-concepto4
¿Si usamos complemento a 2 y tenemos 8 bits cuantos números podemos representar y cuales? La primera pregunta se puede responder facílmente acudiendo a la teoria de la combinatoria, dado que nos encontramos ante un problema de variación con repetición seria cuestion de elevar 2 a la n bits, donde n es la cantidad de bits que puede usarse para representar un número dado..
Pero entonces, ¿como saber el rango de valores representables?
En la representación mediante complemento a 2, el maximo numero que se puede representar cuando hay n digitos binarios es:
Nota aqui que el -1 en la ecuación anterior se debe a que el cero se representa como un “numero positivo”, por lo tanto si pudieramos representar 128 numeros positivos el primer numero seria el cero y el ultimo el 127, esto debido a que de 0 (inclusive) a 127 (inclusive) hay 128 numeros.
Y el minimo numero negativo que se puede representar es:
Este script en Javascript te puede ayudar a calcular muy rapidamente los limites representables.
/*
Sabemos que tenemos n bits y por tanto cuantos numeros se pueden
representar con ellos, una mitad permite representar los numeros positivos y
el 0, pero el 0 tambien se debe representar entonces al max value le debemos
restar 1, en cambio para hallar el minvalue no hay necesidad de restar.
*/
function limits(n) {
return {
maxval: ((2**n)/2)-1,
minval: -1*(2**n)/2
}
}
Si queremos saber cuantos numeros se pueden representar con 8, 16, 32 o cualquier otra cantidad de bits solo seria cuestion de asignar el argumento n en la funcion anterior.
limits(8) // output: {maxval: 127, minval: -128}
limits(16) // output: {maxval: 32767, minval: -32768}
limits(32) // output: {maxval: 2147483647, minval: -2147483648}
Si nosotros intentamos por ejemplo representar mediante complemento a 2 con 4bits un numero que es mayor al maximo valor que se puede representar entonces obtendremos un error, esto debido a que si dicho error no ocurriera entonces un numero en binario representaria dos numeros al mismo tiempo.
| Base 10 | Base 2 (4 bits) | Base 16 | Base 2, Representación mediante complemento a 2 |
|---|---|---|---|
| 0 | 0000 | 0 | 0000 |
| 1 | 0001 | 1 | 0001 |
| 2 | 0010 | 2 | 0010 |
| 3 | 0011 | 3 | 0011 |
| 4 | 0100 | 4 | 0100 |
| 5 | 0101 | 5 | 0101 |
| 6 | 0110 | 6 | 0110 |
| 7 | 0111 | 7 | 0111 |
| 8 | 1000 | 8 | Overflow Error |
| 9 | 1001 | 9 | Overflow Error |
| 10 | 1010 | A | Overflow Error |
| 11 | 1011 | B | Overflow Error |
| 12 | 1100 | C | Overflow Error |
| 13 | 1101 | D | Overflow Error |
| 14 | 1110 | E | Overflow Error |
| 15 | 1111 | F | Overflow Error |
Sumas y restas usando complemento a 2 - concepto5-concepto6
Empecemos con una resta que puede sonar mas dificil, por ejemplo 2-1=2+(-1) es decir simplemente es hallar la representación del 2 y la del -1 en complemento a 2 luego se suman estos numeros en binario y el numero binario resultante es el resultado:
2=0010
-1=1111
11
0010 +
1111
____
0001 (1)
Lo cual tiene mucho sentido, ahora vamos a sumar 2 + 15 y veamos que ocurre:
2=0010
15=1111
11
0010 +
1111
____
0001 (1)
Vemos que nos da otra vez 0001 es decir segun esto 2-1=1 y 15+2=1 ¿Que ha ocurrido? rta/ nada que no se haya explicado ya, empecemos observando que el 15 (uno de los sumandos) es mayor a 7 es decir esta por fuera del rango representable y por consiguiente el resultado tambien lo estara.
Tengase en cuenta que como nuestra salida es de 4 bits ocurre un overflow y se pierde el ultimo bit.
Los computadores y el complemento a 2 - concepto7-concepto8
Basado en lo anterior puedo hacerme la idea de que la mayoria de los computadores usan el complemento a 2 para representar numeros debido a que les permite efectuar tanto sumas como restas usando un unico chip de suma, ahorrando asi el diseño de otros chips mas complejos y especializados.
Diferencias entre un half adder y un full adder - concecpto9
Antes de entrar a la implementación de estos dos chips vamos a discutir algunas diferencias, por un lado el half-adder solo permite sumar un numero de un bit con otro numero de un bit y nos da un resultado de 1 bit, por otro lado, el full-adder nos permite sumar 3 numeros de 1 bit, esta diferencia es importante porque este 3 bit es el que se conoce como carry-in es decir el que en caso de que halla un carry en una suma anterior se encargue sumarlo a los dos primeros bits.
2=0010
-1=1111
11 (carryin or c)
0010 + (a)
1111 (b)
____
0001 (1) (sum)
En lo que a las salidas de estos dos chips notamos que son identicas ambos tienen un sum y un carryout que indica si la suma de los sumandos da un numero mayor a 1 (base2).
Esto es identíco a lo que se veia en la escuela, la única diferencia es que aqui los numeros van del 0 al 1 mientras que en la escuela iban del 0 al 9.
Significado del carry de una suma - concepto10
El carry de una suma es lo que en español se conoce como “lo que llevo”, si por ejemplo sumamos 29 + 12 (base10) empezamos sumando los digitos menos significativos en este caso 9 y 2, 9+2 = “1 y llevo 1” luego ese 1 “que llevo” lo sumo con los siguientes digitos menos significativos en este caso 2 y 1: (2+1)+(“lo que llevo” 1) = 4.
1 (lo que llevo o c)
29 + (a)
12 (b)
____
41 (resultado)
La única diferencia es que cuando sumamos numeros binarios los numeros van de 0 a 1, cuando sumemos dos numeros cuya suma sea mayor a 1 (seria la analogía del 9 en base 10) debemos sumar los LSB y poner “sobre” los siguientes bits menos significativos “lo que llevamos (carry)” para que posteriormente se sume con dichos bits.
Analizando la ALU - concepto11
Mostrar el valor de los pines internos.
Implementando el half adder
NOTA: No pondré tablas de verdad en casos en los que no se amerite.
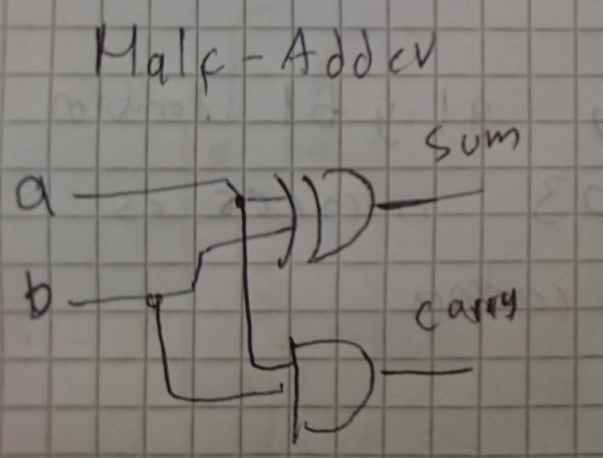

Si analizamos la tabla de verdad del half adder podemos ver que la salida sum es equivalente a un Xor(A, B) y la salida Carry es equivalente a un And(A, B).
CHIP HalfAdder {
IN a, b; // 1-bit inputs
OUT sum, // Right bit of a + b (LSB)
carry; // Left bit of a + b (MSB)
PARTS:
// Put you code here:
And(a=a, b=b, out=carry);
/*
This also is correct:
And(a=a, out=carry, b=b);
*/
Xor(a=a, b=b, out=sum);
}
Implementando el full adder
Como ya fue mencionado anteriormente el full-adder tiene tres entradas de 1 bit donde la 3ra entrada es el carryin es decir el carry (carryout) del full-adder anterior.
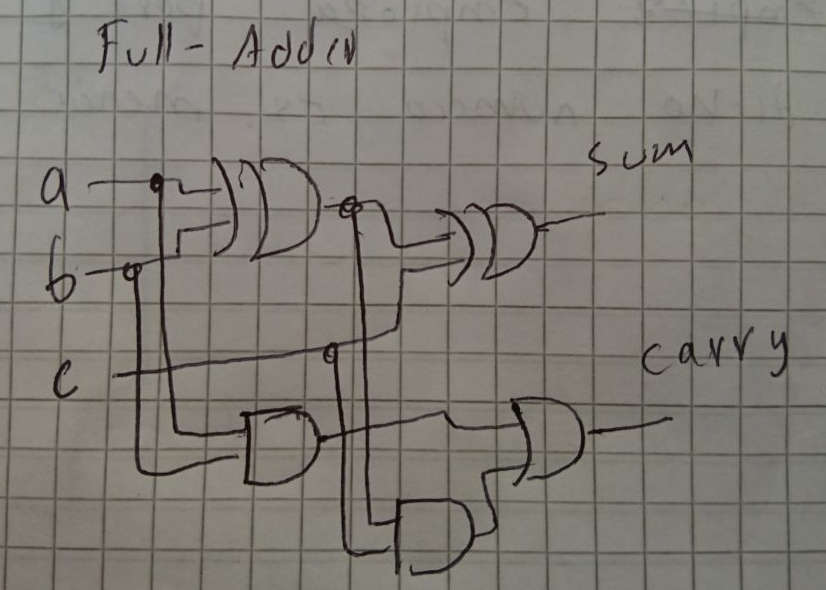
El circuito puede parecer “sin sentido entendible” o “una mera abstracción practica” pero en esta caso la conexión de los chips dentro del full-adder sigue un orden que se explicará a continuación:
- Sumo los sumandos a y b.
- A dicho resultado le sumo el carryin (c) y esto sera lo que saldra por el pin de salida sum.
- Si la suma de los sumandos (a y b) o (el resultado de dicha suma y el carryin) dieron un valor mayor a 1 entonces el pin de salida carry sera 1.
CHIP FullAdder { IN a, b, c; // 1-bit inputs, the c AKA carryIn6 OUT sum, // Right bit of a + b + c carry; // Left bit of a + b + c aka carryOut PARTS: // Put you code here: HalfAdder(a=a, b=b, sum=half1sum, carry=half1carry); HalfAdder(a=c, b=half1sum, sum=sum, carry=half2carry); Or(a=half1carry, b=half2carry, out=carry); }
Implementando el 16-bit Adder
En este punto el 16-bit adder no debe requerir mucha explicación puesto que esta implementación unicamente consiste de encadenar varios full-adder.
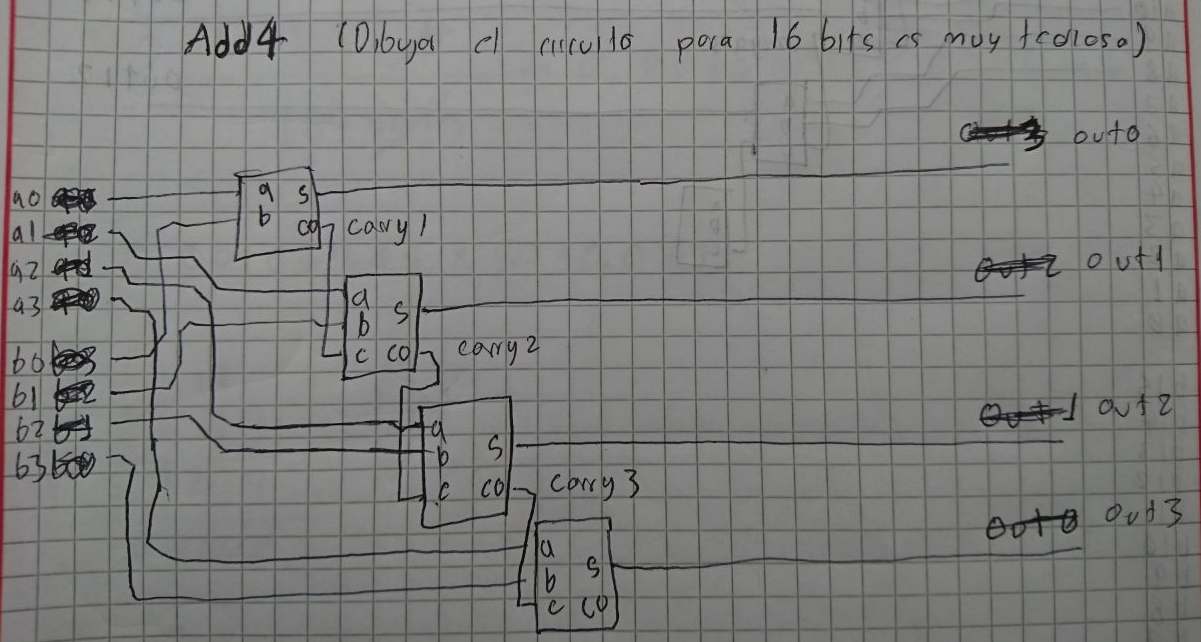
Nota1: El circuito que se muestra suma dos numeros de 4-bits por cuestiones de optimización de tiempo en el dibujado, el circuito seria el mismo solo que con 16 full-adders.
Nota2: Como se esta representando el complemento a 2 como técnica de representación númerica la salida es de 4 bits y los valores a sumar (por tanto el resultado) estan restringidos por el rango [-128, 127].
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
// Put you code here:
// I am going to chain multiple full adder.
HalfAdder(a=a[0], b=b[0], sum=out[0], carry=carry0);
FullAdder(a=a[1], b=b[1], c=carry0, sum=out[1], carry=carry1);
FullAdder(a=a[2], b=b[2], c=carry1, sum=out[2], carry=carry2);
FullAdder(a=a[3], b=b[3], c=carry2, sum=out[3], carry=carry3);
FullAdder(a=a[4], b=b[4], c=carry3, sum=out[4], carry=carry4);
FullAdder(a=a[5], b=b[5], c=carry4, sum=out[5], carry=carry5);
FullAdder(a=a[6], b=b[6], c=carry5, sum=out[6], carry=carry6);
FullAdder(a=a[7], b=b[7], c=carry6, sum=out[7], carry=carry7);
FullAdder(a=a[8], b=b[8], c=carry7, sum=out[8], carry=carry8);
FullAdder(a=a[9], b=b[9], c=carry8, sum=out[9], carry=carry9);
FullAdder(a=a[10], b=b[10], c=carry9, sum=out[10], carry=carry10);
FullAdder(a=a[11], b=b[11], c=carry10, sum=out[11], carry=carry11);
FullAdder(a=a[12], b=b[12], c=carry11, sum=out[12], carry=carry12);
FullAdder(a=a[13], b=b[13], c=carry12, sum=out[13], carry=carry13);
FullAdder(a=a[14], b=b[14], c=carry13, sum=out[14], carry=carry14);
FullAdder(a=a[15], b=b[15], c=carry14, sum=out[15], carry=carry15);
}
Implementando el 16-bit Incrementer
Para esto se usó un Add16 con una entrada variable y la otra constante: 1 (base10).
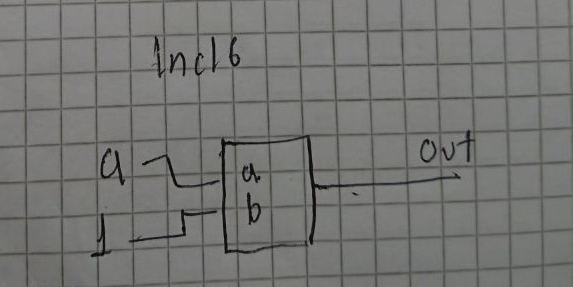
Es importante tener en cuenta el valor que se asigna a los pines de la entrada constante:
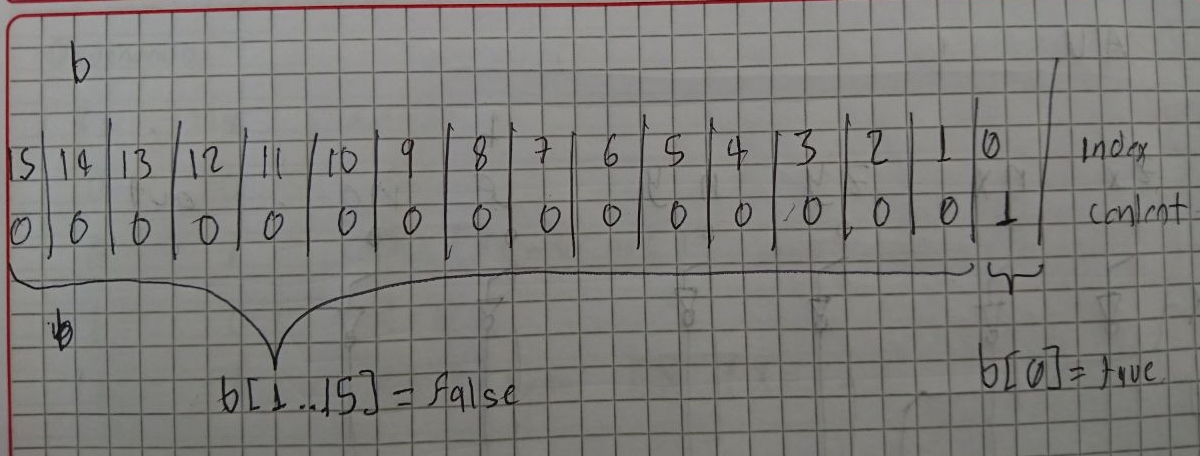
Si en lugar de lo anterior hicieramos:
b=true
El valor constante seria
1111 1111 1111 1111
El cual representa un -1 por lo tanto estariamos haciendo un decrementer.
Implementando la ALU
El objetivo de este chip es: dada unas entradas x e y y unos pines de configuración realizar sobre x e y la operación determinada y dar su resultado por el pin de salida out, ademas, si la salida fue menor a 0 un segundo pin de salida debe dar 1, y si fue igual a 0 un tercer pin debe devolver 1.
Para solucionar el problema anterior se decidió usar varios Mux16 como selectores y dividir el problema en partes:
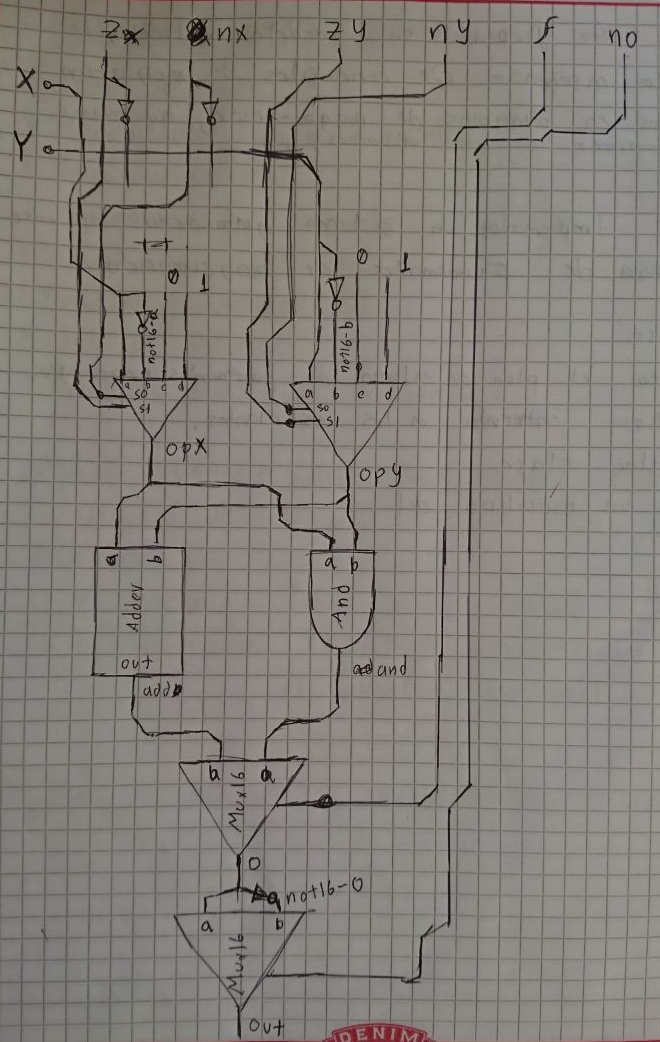
Se puede ver que zx y nx pueden permitir 4 operaciones distintas sobre la entrada X
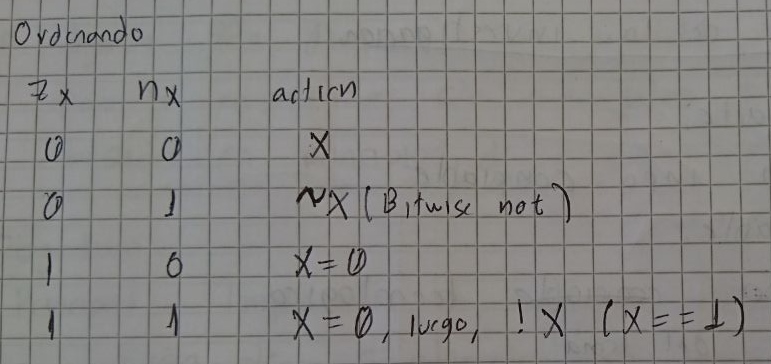
Entonces podemos usar un Mux4Way16, donde los pines de selección sean nx y zx, y las entradas sean las distintas operaciones que se pueden efectuar sobre el pin de entrada X
Ademas se observa que el tercer caso es false siempre y el cuarto es true siempre.
El mismo procedimiento se puede seguir para zy y ny, luego a las dos salidas resultantes de estos dos Mux4Way16 las introduzco a un Add16 y a un And16.
De nuevo, estas dos salidas las introduzco en otro Mux16 donde el pin de seleccion este conectado al pin f y por último meto a otro Mux16 esta salida, solo que aplico el operador complemento (Not16) a una de ellas, asi tengo la version normal y la versión negada.
Para implementar los pines de salida indicadores de estado se hizo uso de la propiedad identidad de los Or y se implementaron 2 chips que se considero necesarios para la solución.
CHIP ALU {
IN
x[16], y[16], // 16-bit inputs
zx, // zero the x input?
nx, // negate the x input?
zy, // zero the y input?
ny, // negate the y input?
f, // compute out = x + y (if 1) or x & y (if 0)
no; // negate the out output?
OUT
out[16], // 16-bit output
zr, // 1 if (out == 0), 0 otherwise
ng; // 1 if (out < 0), 0 otherwise
PARTS:
// Put you code here:
Not16(in=x, out=not16-x);
Not16(in=y, out=not16-y);
// d=1111111111111111
// c=0000000000000000
Mux4Way16(a=x, b=not16-x, c=false, d=true, sel[0]=nx, sel[1]=zx, out=opx);
Mux4Way16(a=y, b=not16-y, c=false, d=true, sel[0]=ny, sel[1]=zy, out=opy);
Add16(a=opx, b=opy, out=add);
And16(a=opx, b=opy, out=and);
Mux16(a=and, b=add, sel=f, out=o);
//Mux16(a=add, b=and, sel=f, out=o);
Not16(in=o, out=noto);
Mux16(a=o, b=noto, sel=no, out=aluout);
Equivalence16(a=aluout, b[0..15]=false, out=zr);
NotGreatThanZero(in=aluout, out=ng); // ng: not great than
// A | false = A, indentity property in or
Or16(a=aluout, b[0..15]=false, out=out);
}
Dicha solución consistió en tomar la salida de la ALU (el out del último Mux16) y pasarlo por un chip que en un lenguaje de alto nivel tipo c++ seria == el cual devuelve true, unicamente cuando el “left-hand-term” y el “right-hand-term” son iguales, notese que este chip debe recibir dos numeros de 16-bits y devolver un único bit ¿como implementar esto? rta/ para que dos numeros de n bits sean iguales debe cumplirse que a[n-1] sea igual a b[n-1] y a[n-2] sea igual a b[n-2] … y a[0] sea igual a b[0].
Es decir se necesita de un chip que reciba dos inputs y devuelva true solo cuando los valores en dichos inputs son iguales, para esto se uso la función equivalencia que es la opuesta a la función Xor, he aqui la implementación:
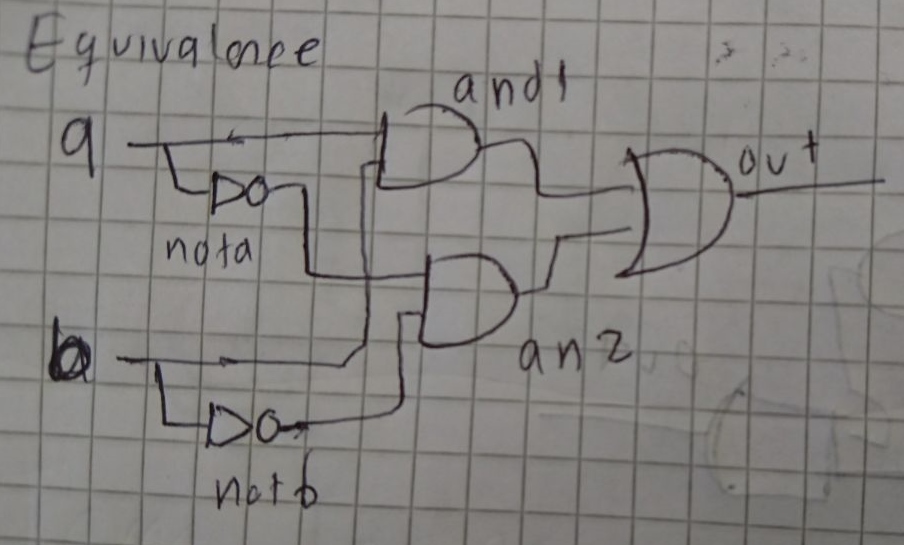
CHIP Equivalence {
IN a, b;
OUT out;
PARTS:
And(a=a, b=b, out=and1);
Not(in=a, out=nota);
Not(in=b, out=notb);
And(a=nota, b=notb, out=and2);
Or(a=and1, b=and2, out=out);
}
Y la implementación del Equivalence16:
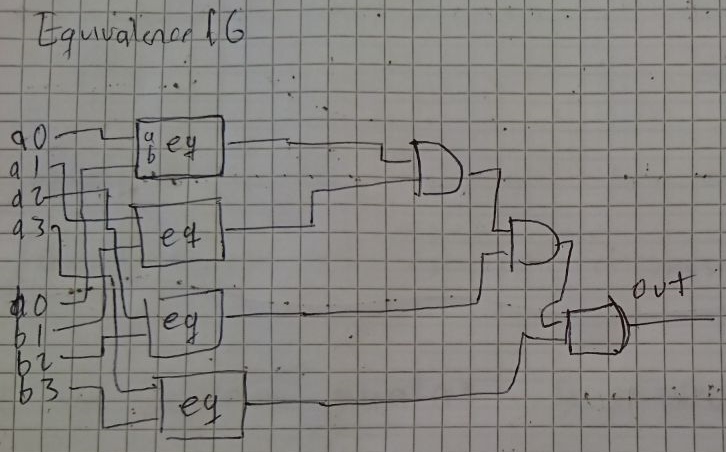
// Same as == operator in high level langagues
// ex: 5==5 => true
CHIP Equivalence16 {
IN
a[16], b[16];
OUT
out;
PARTS:
Equivalence(a=a[0], b=b[0], out=iseqbit0);
Equivalence(a=a[1], b=b[1], out=iseqbit1);
Equivalence(a=a[2], b=b[2], out=iseqbit2);
Equivalence(a=a[3], b=b[3], out=iseqbit3);
Equivalence(a=a[4], b=b[4], out=iseqbit4);
Equivalence(a=a[5], b=b[5], out=iseqbit5);
Equivalence(a=a[6], b=b[6], out=iseqbit6);
Equivalence(a=a[7], b=b[7], out=iseqbit7);
Equivalence(a=a[8], b=b[8], out=iseqbit8);
Equivalence(a=a[9], b=b[9], out=iseqbit9);
Equivalence(a=a[10], b=b[10], out=iseqbit10);
Equivalence(a=a[11], b=b[11], out=iseqbit11);
Equivalence(a=a[12], b=b[12], out=iseqbit12);
Equivalence(a=a[13], b=b[13], out=iseqbit13);
Equivalence(a=a[14], b=b[14], out=iseqbit14);
Equivalence(a=a[15], b=b[15], out=iseqbit15);
And(a=iseqbit0, b=iseqbit1, out=and0);
And(a=and0, b=iseqbit2, out=and1);
And(a=and1, b=iseqbit3, out=and2);
And(a=and2, b=iseqbit4, out=and3);
And(a=and3, b=iseqbit5, out=and4);
And(a=and4, b=iseqbit6, out=and5);
And(a=and5, b=iseqbit7, out=and6);
And(a=and6, b=iseqbit8, out=and7);
And(a=and7, b=iseqbit9, out=and8);
And(a=and8, b=iseqbit10, out=and9);
And(a=and9, b=iseqbit11, out=and10);
And(a=and10, b=iseqbit12, out=and11);
And(a=and11, b=iseqbit13, out=and12);
And(a=and12, b=iseqbit14, out=and13);
And(a=and13, b=iseqbit15, out=out);
}
Volviendo al problema original de la ALU con el pin de salida zr hallar una solución fue trivial una vez se contó con el chip Equivalencia16.
Quedaba por resolver el problema de como implementar el funcionamiento del pin ng, para esto se diseño otro chip especial, el cual fue llamado NotGreatThan, su funcionamiento parte de la observación de que en la representación por complemento a 2 siempre se cumple que el MSB siempre es igual a 1 por lo tanto cualquier numero menor a 0 a su vez cumple la misma condición, por lo tanto, haciendo uso del chip Equivalence se diseño un chip que averiguara si el MSB era igual a 1 y devolviera dicho resultado.
CHIP NotGreatThanZero {
IN
in[16];
OUT
out;
PARTS:
Equivalence(a=in[15], b=true, out=out);
}
…Y se uso este chip con el mismo procedimiento, pasando a su pin de entrada el aluout y conectando su salida al pin de salida ng de la ALU.
Por ultimo como se necesitaba devolver por el out de la ALU el valor en aluout sin ningun tipo de procesamiento extra, se usó la propiedad identidad de los Or, es decir:
aluout | 0 == aluout // true siempre.
Donde la salida del Or se conectó al out de la ALU, a continuación se muestra una tabla donde se detallan 12 operaciones que esta ALU puede realizar:
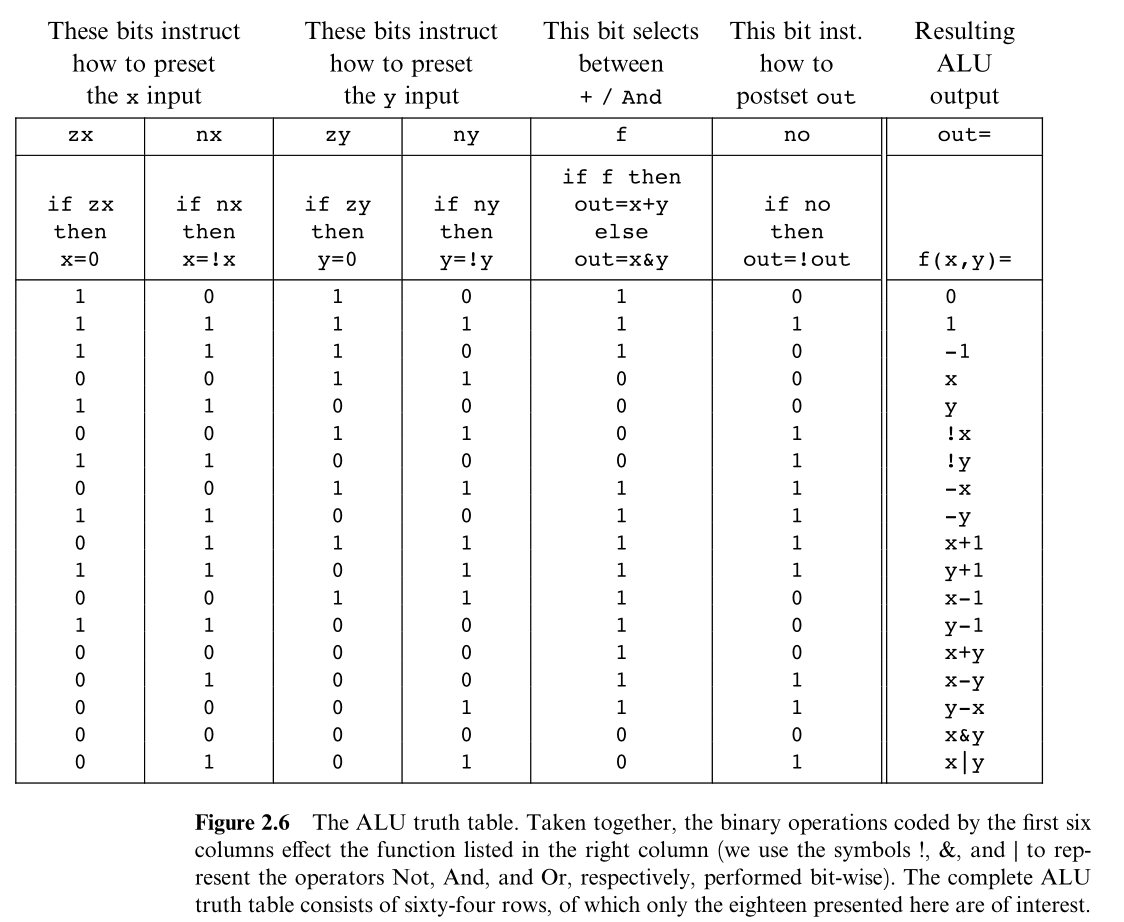
Nota1: Esta implementación esta pecando de complejidad en los pines de salida zr y ng.
Demostracion teorica del OR y otras operaciones con esta ALU
¿Como es posible que la ALU que hemos implementado realice tantas operaciones?
Vamos a intentar explicar solo algunas:
-X
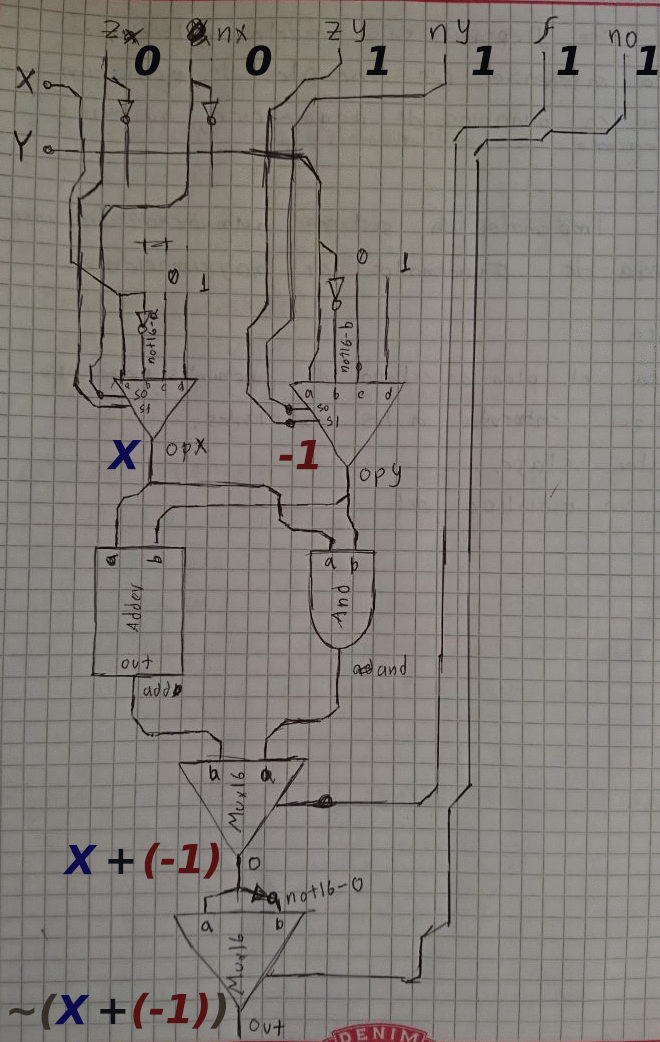
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
X+1
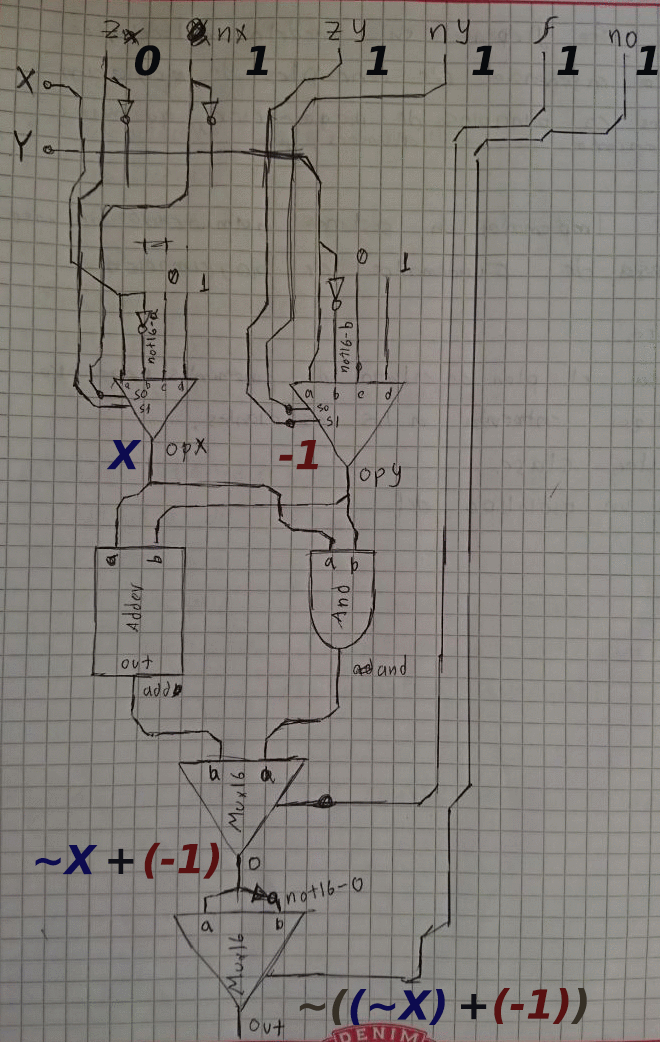
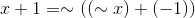
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
X-Y
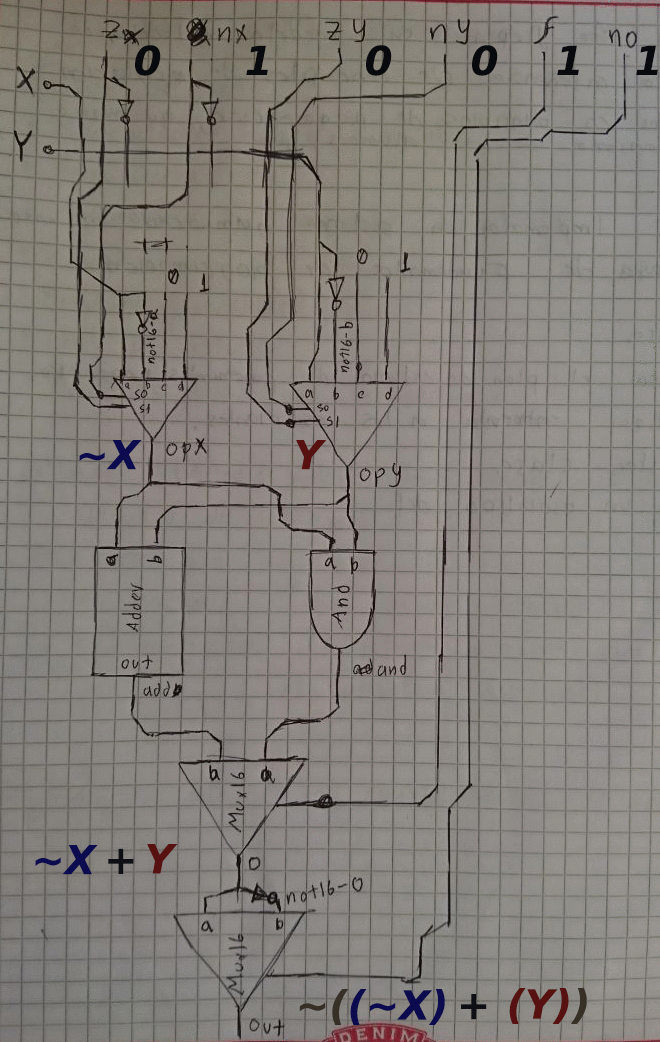
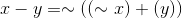
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
X | Y
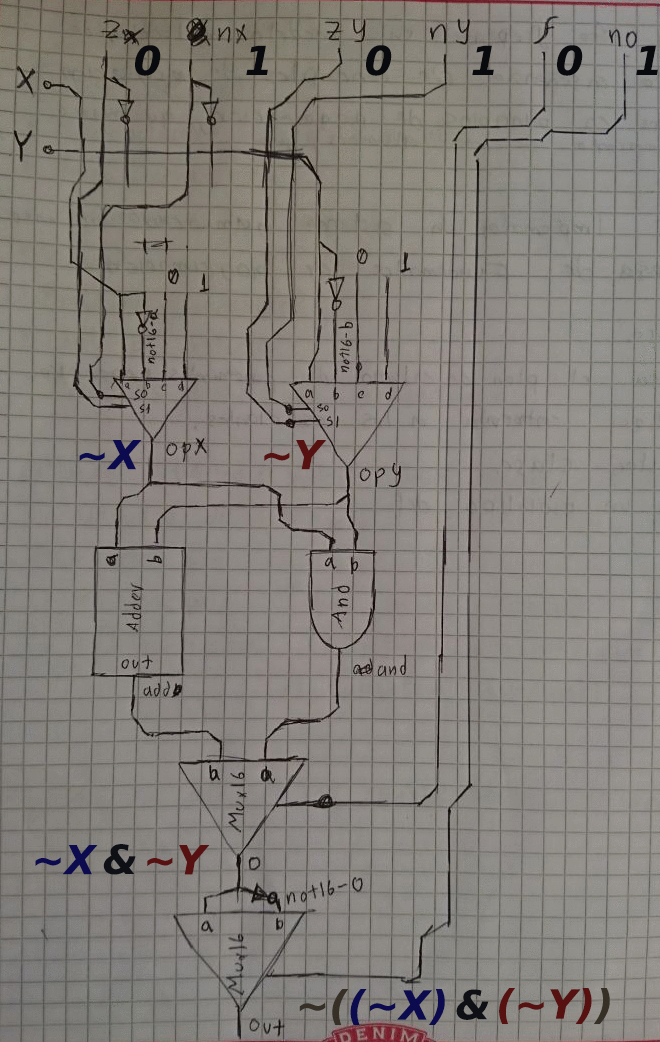
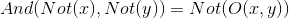
.gif)
.gif)
Nota: En este caso se parte de una ley conocida como la ley de morgan.

